Methoden der EWF

Die folgenden Packages wurden für das Erstellen dieses Dokuments verwendet:

Code 
library(pracma)
library(MASS)
library(lmtest)
library(numDeriv)
library(tidyverse)
library(L1pack)
library(ggpubr)
library(AER)
library(sem)
library(maxLik)

Lineare Regression (Vertiefung)

Gauss-Markov-Theorem

Das Gauss-Markov-Theorem besagt, dass der OLS Schätzer \(\beta=(X^TX)^{-1}X^Ty\) der best linear unbiased estimator (BLUE) ist. Das bedeutet, es gibt keinen anderen Schätzer in dieser Familie, welcher eine geringere Varianz aufweißt.

ACHTUNG: Der hier genutzte Least Absolute Deviations (LAD) Schätzer gehört nicht zu den linearen Schätzern und sollte daher eigentlich nicht zum Vergleich genutzt werden. Die folgenden Simulationen dienen also nur dazu, das Verhalten von OLS zu LAD bei verschiedenen Verteilungen der Residuen zu zeigen. Gleichzeitig ist auch zu erkennen, dass OLS nicht immer der beste Schätzer ist (auch wenn es manchmal so aussieht).

Simulation mit normalverteilten Residuen.

Code 
n <- 100
x <- seq(from = 0, to = 10, length.out = n)
n_runs <- 10000
beta <- cbind(numeric(n_runs), numeric(n_runs))
for(i in 1:n_runs){
  u <- rnorm(n, mean = 0, sd = 2)
  y <- x + u
  
  R_OLS <- lm(y ~ x)
  beta[i, 1] <- R_OLS$coefficients[2]
  
  R_LAD <- lad(y ~ x)
  beta[i, 2] <- R_LAD$coefficients[2]
}

beta %>%
  data.frame() %>%
  rename("OLS" = X1, "LAD" = X2) %>%
  pivot_longer(cols = OLS:LAD) %>%
  ggplot(aes(x = value, color = name))+
  geom_density()+
  geom_vline(xintercept = 1, linetype = "dashed")+
  coord_cartesian(xlim = c(.5,1.5), ylim = c(0, 8))+
  theme_bw()+
  theme(legend.position = "top")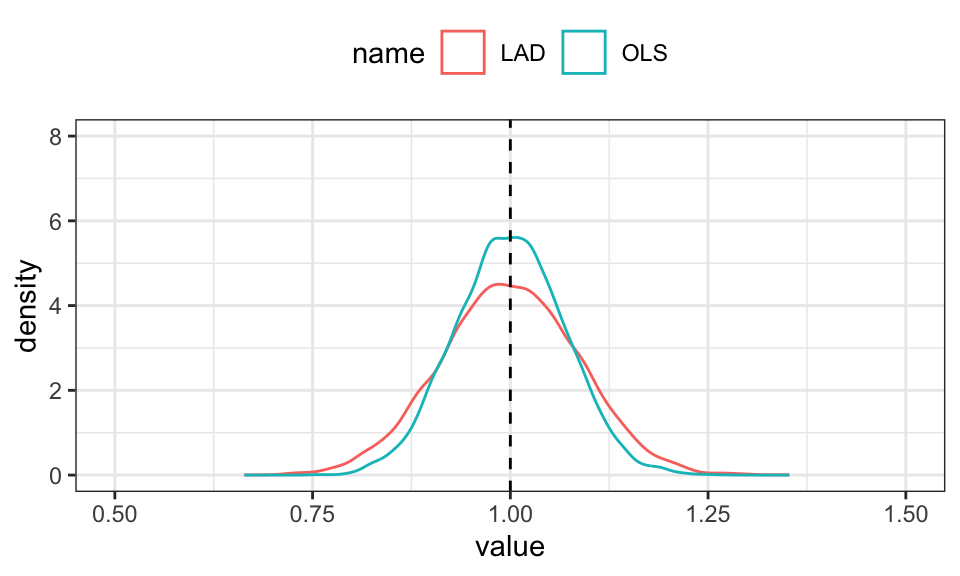

Simlation mit exponentialverteilten und mittelwertzentrierten Residuen.

Code 
n <- 100
x <- seq(from = 0, to = 10, length.out = n)
n_runs <- 10000
beta <- cbind(numeric(n_runs), numeric(n_runs))
for(i in 1:n_runs){
  u <- scale(rexp(n, rate = .5), scale = FALSE)
  y <- x + u
  
  R_OLS <- lm(y ~ x)
  beta[i, 1] <- R_OLS$coefficients[2]
  
  R_LAD <- lad(y ~ x)
  beta[i, 2] <- R_LAD$coefficients[2]
}

beta %>%
  data.frame() %>%
  rename("OLS" = X1, "LAD" = X2) %>%
  pivot_longer(cols = OLS:LAD) %>%
  ggplot(aes(x = value, color = name))+
  geom_density()+
  geom_vline(xintercept = 1, linetype = "dashed")+
  coord_cartesian(xlim = c(.5,1.5), ylim = c(0, 8))+
  theme_bw()+
  theme(legend.position = "top")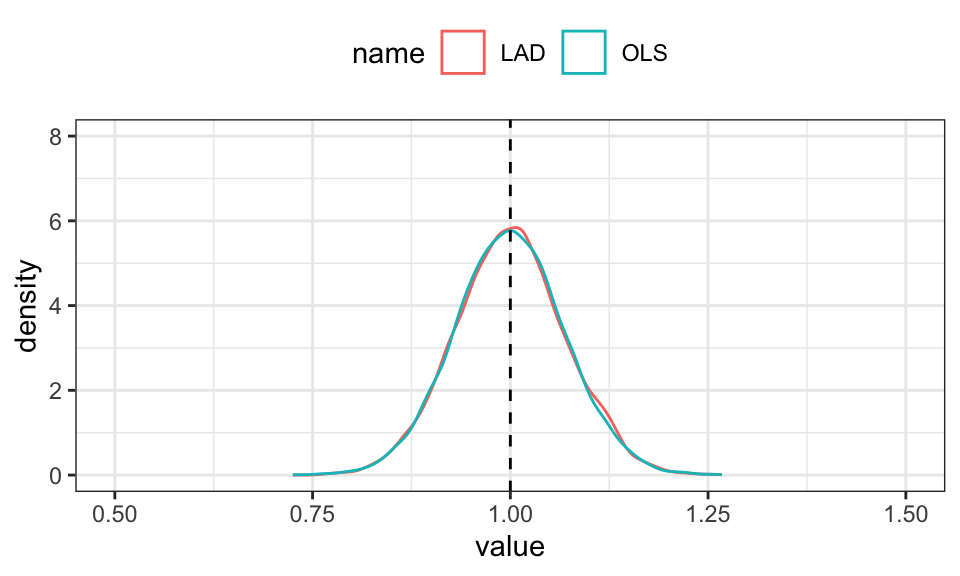

Simulation mit t-verteilten Residuen.

Code 
n <- 100
x <- seq(from = 0, to = 10, length.out = n)
n_runs <- 10000
beta <- cbind(numeric(n_runs), numeric(n_runs))
for(i in 1:n_runs){
  u <- rt(n, 2)
  y <- x + u
  
  R_OLS <- lm(y ~ x)
  beta[i, 1] <- R_OLS$coefficients[2]
  
  R_LAD <- lad(y ~ x)
  beta[i, 2] <- R_LAD$coefficients[2]
}

beta %>%
  data.frame() %>%
  rename("OLS" = X1, "LAD" = X2) %>%
  pivot_longer(cols = OLS:LAD) %>%
  ggplot(aes(x = value, color = name))+
  geom_density()+
  geom_vline(xintercept = 1, linetype = "dashed")+
  coord_cartesian(xlim = c(.5,1.5), ylim = c(0, 8))+
  theme_bw()+
  theme(legend.position = "top")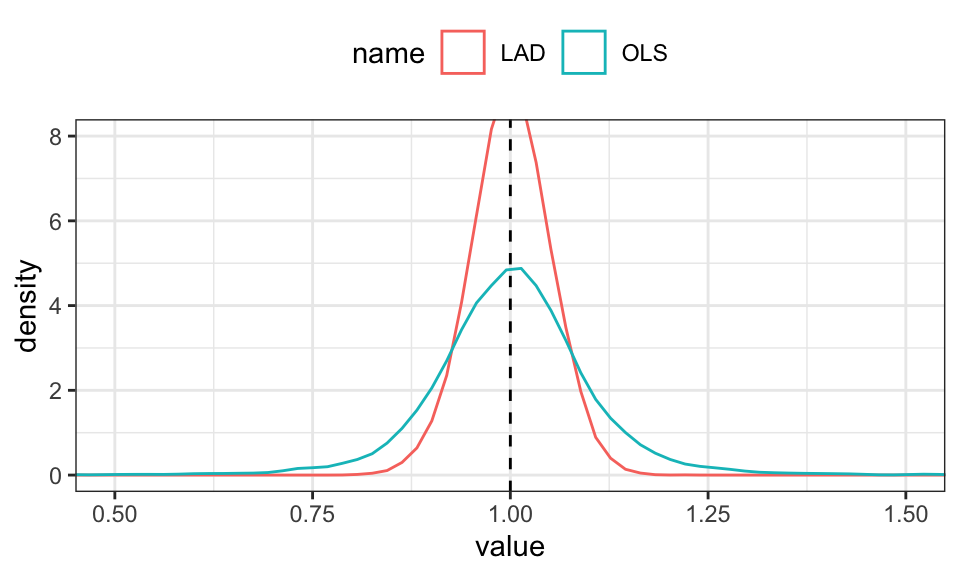

Konsistenz

Code 
ns <- c(10, 100, 500)
n_runs <- 10000
beta <- matrix(rep(0, length(ns) * n_runs), ncol = length(ns))

for (j in 1:length(ns)) {
  n <- ns[j]
  x <- seq(from = 0, to = 10, length.out = n)
  
  for (i in 1:n_runs) {
    u <- rnorm(n, mean = 0, sd = 3)
    y <- 5 + 2 * x + u
    
    beta[i, j] <- coef(lm(y ~ x))[2]
  }
}

beta %>%
  data.frame() %>%
  rename("10" = X1, "100" = X2, "500" = X3) %>%
  pivot_longer(cols = everything(), names_to = "Anzahl_Beobachtungen", values_to = "beta") %>%
  ggplot(aes(x = beta, color = Anzahl_Beobachtungen))+
  geom_density()+
  geom_vline(xintercept = 2, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top")+
  labs(color = "Anzahl Beobachtungen")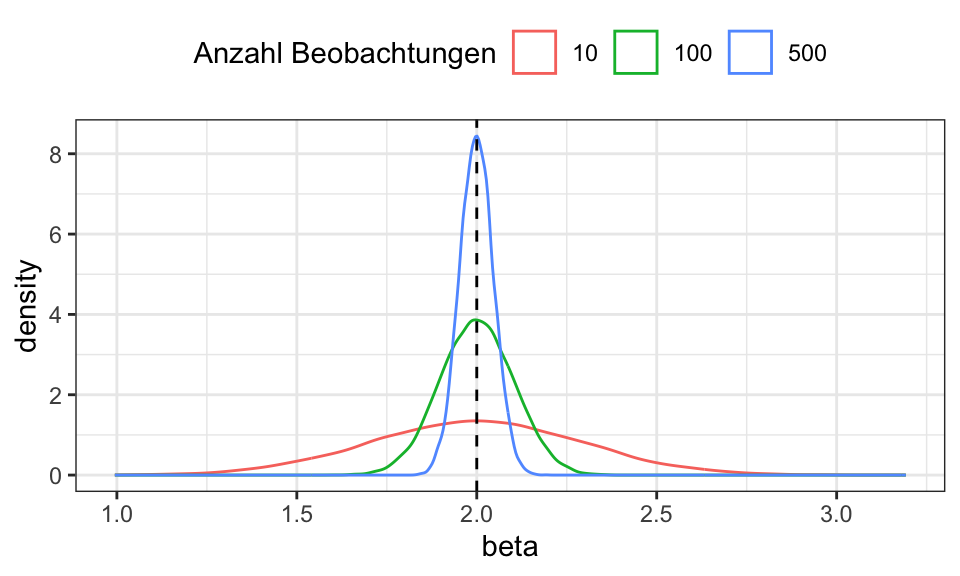

Ein erwartungstreuer und konsistenter Schätzer ist sozusagen der Musterschüler unter den Schätzern: Selbst für kleine Stichproben liefert er im Mittel den wahren Wert und mit größeren Stichproben sinkt noch die Streuung: \(E(\hat{\beta}) = \beta\) und \(Var(\hat{\beta}) = \frac{\sigma^2}{n} = 0\) für \(n \rightarrow \infty\)

Code 
ns <- c(10, 100, 500)
n_runs <- 10000
beta <- matrix(rep(0, length(ns) * n_runs), ncol = length(ns))

for (j in 1:length(ns)) {
  n <- ns[j]
  x <- seq(from = 0, to = 10, length.out = n)
  
  for (i in 1:n_runs) {
    u <- rnorm(n, mean = 0, sd = 3)
    y <- 5 + 2 * x + u
    
    beta[i, j] <- coef(lm(y ~ x))[2] - 5/n
  }
}

beta %>%
  data.frame() %>%
  rename("10" = X1, "100" = X2, "500" = X3) %>%
  pivot_longer(cols = everything(), names_to = "Anzahl_Beobachtungen", values_to = "beta") %>%
  ggplot(aes(x = beta, color = Anzahl_Beobachtungen))+
  geom_density()+
  geom_vline(xintercept = 2, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top")+
  labs(color = "Anzahl Beobachtungen")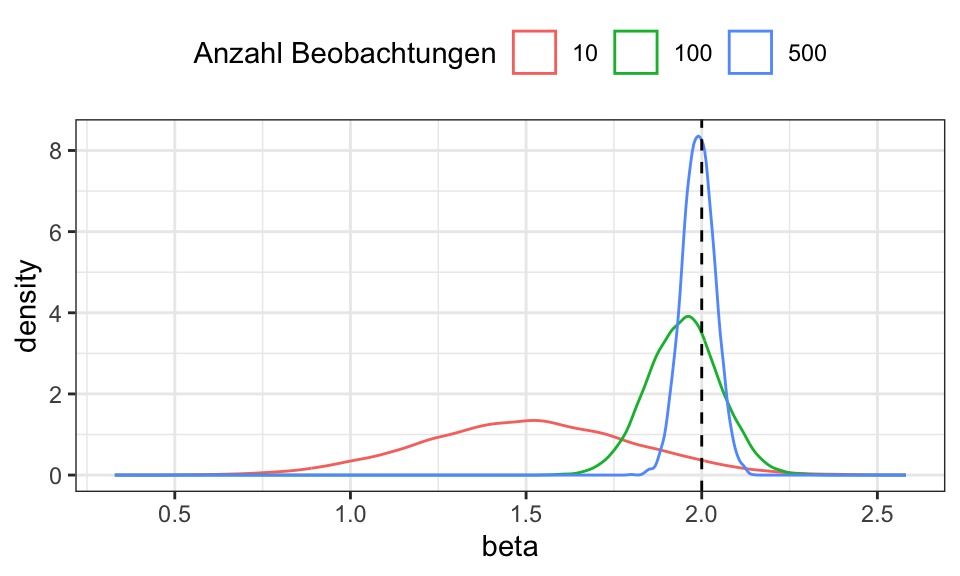

Ein verzerrter, aber konsistenter Schätzer hat zwar einen verzerrten Erwartungswert, welcher aber gegen den wahren Erwartungswert strebt: \(E(\hat{\beta}) = \beta - \frac{5}{n} = \beta\) für \(n \rightarrow \infty\). Zusätzlich geht auch die Varianz gegen Null: \(Var(\hat{\beta}) = \frac{\sigma^2}{n} = 0\) für \(n \rightarrow \infty\).

Code 
ns <- c(10, 20, 30)
n_runs <- 10000
beta <- matrix(rep(0, length(ns) * n_runs), ncol = length(ns))

for (j in 1:length(ns)) {
  n <- ns[j]
  x <- runif(n, min = 0, max = 10)
  
  for (i in 1:n_runs) {
    u <- rnorm(n, mean = 0, sd = 3)
    y <- 0 + u
    
    beta[i, j] <- y[1]
  }
}

beta %>%
  data.frame() %>%
  rename("10" = X1, "20" = X2, "30" = X3) %>%
  pivot_longer(cols = everything(), names_to = "Anzahl_Beobachtungen", values_to = "beta") %>%
  ggplot(aes(x = beta, color = Anzahl_Beobachtungen))+
  geom_density()+
  geom_vline(xintercept = 0, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top")+
  labs(color = "Anzahl Beobachtungen")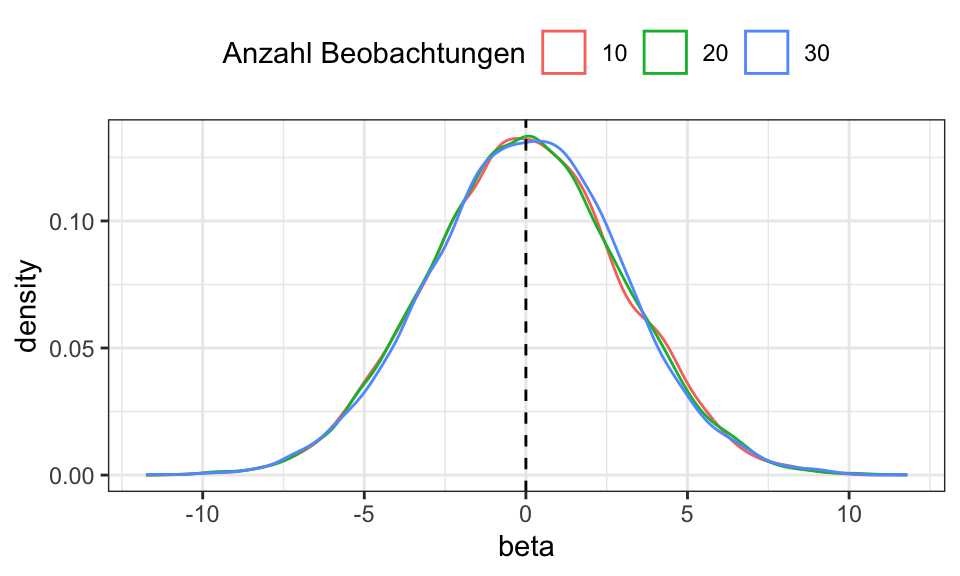

Ein Beispiel für einen nicht-konsistenten (aber erwartungstruen) Mittelwertschätzer ist \(\bar{y} = y_1\), es wird also einfach die erste Beobachtung als der Mittelwert angenommen. Logischerweise ändert sich die Varianz dieses Schätzers mit zunehmend großem Stichprobenumfang nicht: \(Var(\hat{\beta}) = \sigma^2\) auch für \(n \rightarrow \infty\).

Code 
ns <- c(10, 20, 30)
n_runs <- 10000
beta <- matrix(rep(0, length(ns) * n_runs), ncol = length(ns))

for (j in 1:length(ns)) {
  n <- ns[j]
  x <- runif(n, min = 0, max = 10)
  
  for (i in 1:n_runs) {
    u <- rnorm(n, mean = 0, sd = 3)
    y <- 0 + u
    
    beta[i, j] <- y[1] + 5
  }
}

beta %>%
  data.frame() %>%
  rename("10" = X1, "20" = X2, "30" = X3) %>%
  pivot_longer(cols = everything(), names_to = "Anzahl_Beobachtungen", values_to = "beta") %>%
  ggplot(aes(x = beta, color = Anzahl_Beobachtungen))+
  geom_density()+
  geom_vline(xintercept = 0, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top")+
  labs(color = "Anzahl Beobachtungen")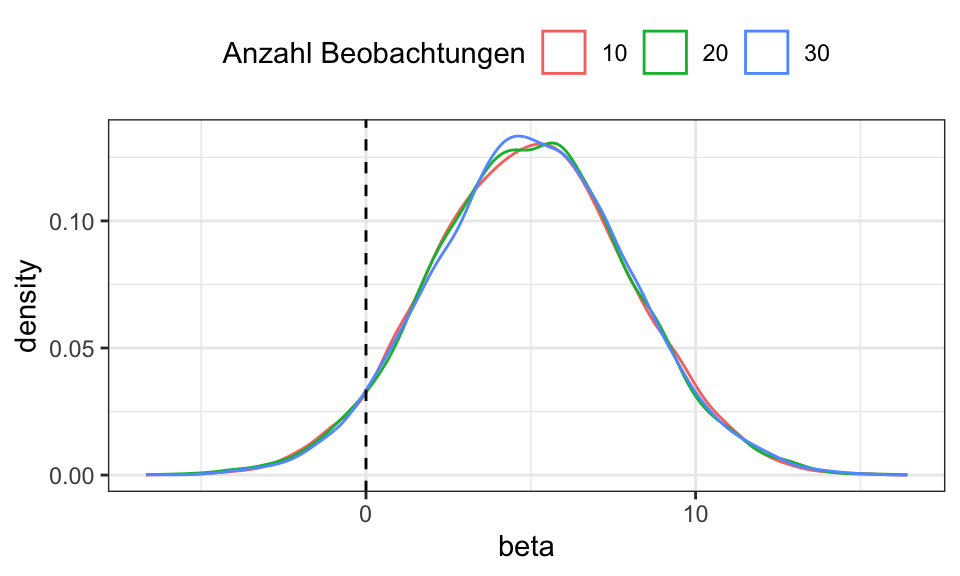

Ein Beispiel für einen nicht-konsistenten (aber erwartungstruen) Mittelwertschätzer ist \(\bar{y} = y_1 + 5\), es wird also einfach die erste Beobachtung + 5 als der Mittelwert angenommen. Logischerweise ändert sich die Varianz dieses Schätzers mit zunehmend großem Stichprobenumfang nicht.

Skalierung des Schätzers

Um die Konsistenz eines Schätzers besser zu zeigen, kann dieser mit \(\sqrt{n}\) multipliziert werden. Dadurch bleibt die Varianz mit steigendem Stichprobenumfang konstant.

Code 
ns <- c(10, 100, 500)
n_runs <- 10000
beta <- matrix(rep(0, length(ns) * n_runs), ncol = length(ns))
beta_scaled <- matrix(rep(0, length(ns) * n_runs), ncol = length(ns))
beta_true <- 5

for (j in 1:length(ns)) {
  n <- ns[j]
  
  for (i in 1:n_runs) {
    u <- rnorm(n, mean = 0, sd = 3)
    y <- beta_true + u
    
    beta[i, j] <- (coef(lm(y ~ 1))[1] - beta_true)
    beta_scaled[i, j] <- (coef(lm(y ~ 1))[1] - beta_true) * sqrt(n)
  }
}

data <- beta %>%
  data.frame() %>%
  rename("10" = X1, "100" = X2, "500" = X3) %>%
  pivot_longer(cols = everything(), names_to = "Anzahl_Beobachtungen", values_to = "beta") %>%
  mutate(is_scaled = "nicht skaliert")


data_scaled <- beta_scaled %>%
  data.frame() %>%
  rename("10" = X1, "100" = X2, "500" = X3) %>%
  pivot_longer(cols = everything(), names_to = "Anzahl_Beobachtungen", values_to = "beta") %>%
  mutate(is_scaled = "skaliert")

bind_rows(data, data_scaled) %>%
  ggplot(aes(x = beta, color = Anzahl_Beobachtungen))+
  geom_density()+
  facet_wrap(~is_scaled, scales = "free")+
  theme_bw()+
  theme(legend.position = "top")+
  labs(color = "Anzahl Beobachtungen")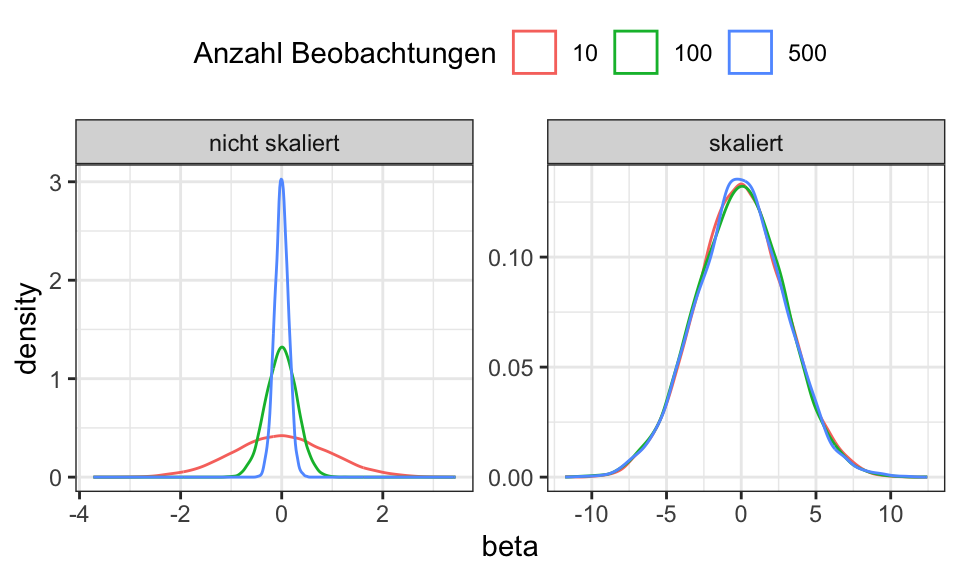

Maximum Likelihood

Bei einer Maximum Likelihood Schätzung wird derjenige Parameter als Schätzung ausgewählt, gemäß dessen Verteilung die Realisierung der beobachteten Daten am plausibelsten erscheint. Dafür muss also zuerst eine Verteilungsannahme, z.B. Normalverteilung \(y_i \sim N(\mu, \sigma^2)\), getroffen werden. Anschließend kann die Dichte einer Beobachtung \(f(x_i| \theta)\) und die der Stichprobe \(f(x_1,…x_n | \theta) = \prod_{i=1}^n f(x_i|\theta)\). Nun wird der Parameter \(\theta\) gesucht, der diese Dichte maximiert.

Für einfachere numerische Approximation wird meist die Log-Likelihood Funktion \(LL(\theta) = \text{log}(\prod_{i=1}^n f(x_i|\theta)) = \sum_{i=1}^n \text{log}(f(x_i | \theta))\) verwendet, da die Likelihood Funktion durch das Produkt sehr schnell sehr klein wird, was zu numerischen Problemen (der Computer kann nur eine begrenzte Anzahl an Nachkommastellen speichern) führt.

Beispiel: Normalverteilung

Für eine Schätzung der Parameter einer Normalverteilung wird zuerst die Dichtefunktion aufgestellt \[f(y_i | \mu, \sigma) = (2\pi \sigma^2)^{-1/2} \text{exp}(-\frac{1}{2}((y_i - \mu)/\sigma)^2)\] und aus dieser ergibt sich dann die Dichte der Stichprobe \[f(y_1, …, y_n | \mu, \sigma) = \prod_{i=1}^n f(y_i | \mu, \sigma) = (2\pi \sigma^2)^{-1/2} \text{exp}(-\frac{1}{2} \sum_{i=1}^n ((y_i - \mu)/\sigma)^2)\] Da das Produkt schnell zu sehr niedrigen Werten führen kann, wird stattdessen der Logarithmus verwendet \[LL(\mu, \sigma | y_1, …, y_n) = -\frac{n}{2} \ln(2\pi) - n \ln \sigma - \frac{1}{2}\sigma^2 \sum_{i=1}^n(y_i-\mu)^2\] Für die numerische Optimierung in R wird die optim() Funktion verwendet, welche ein Minimum sucht. Daher wird die negative Log-Likelihood Funktion verwendet.

Code 
n <- 1000
y <- rnorm(n, mean = 7, sd = 4)

log_L <- function(theta, y) {
  mu <- theta[1]
  sigma <- theta[2]
  -(n/2) * log(2*pi) - n * log(sigma) - (1/2) * sigma^(-2) * sum((y - mu)^2)
}

R <- optim(par = c(mu = 5, sigma = 5), fn = log_L, y = y, control = list(fnscale = -1))
R$par
      mu    sigma 
7.020372 3.948059

Lineare Regression

Ein Vorteil von Maximum Likelihood im Vergleich zu OLS ist, dass die Varianz direkt mitgeschätzt wird.

Die Dichte einer Beobachtung in einem Linearen Regressionsmodell ergibt sich zu \(y \sim N(\mathbf{x}_i^\prime \mathbf{\beta}, \sigma^2)\). Daraus wird die (Log)-Likelihood Funktion aufgestellt.

Code 
n <- 100
n_runs <- 1000
beta <- matrix(numeric(n_runs*3), ncol = 3)

for(i in 1:n_runs){
  x <- runif(n, min = 0, max = 10)
  X <- cbind(1, x)
  y <- 2 + 4*x + rnorm(n, mean = 0, sd = 2)
  
  LL <- function(param) {
      beta <- param[1:2]
      sigma <- param[3]
      -n/2 * log(2*pi*sigma^2) - 1/(2*sigma^2) * sum((y - X %*% beta)^2)
  }
  
  beta_start <- c(1,1)
  sigma_start <- 1
  R <- maxLik(LL, start = c(beta_start, sigma_start))
  beta[i,] <- coef(R)
}

beta %>%
  data.frame() %>%
  rename("beta_1" = X1, "beta_2" = X2, "sigma" = X3) %>%
  pivot_longer(cols = everything()) %>%
  ggplot(aes(x = value))+
  geom_density()+
  facet_wrap(~name, scales = "free_x")+
  theme_bw()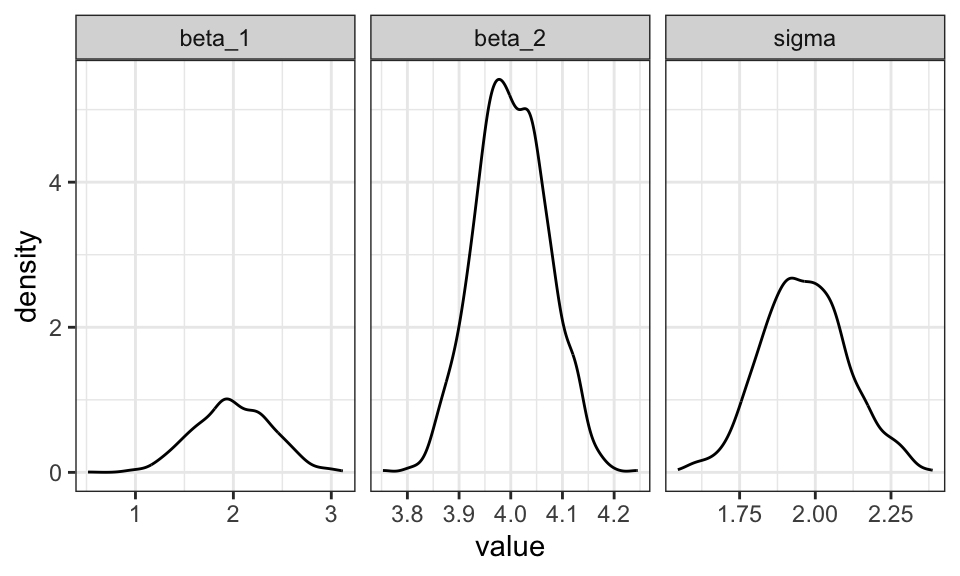

Likelihood vs Log-Likelihood

Code 
set.seed(123)
n <- 2
mu <- 2
sigma <- 1.5
data <- rnorm(n, mean = mu, sd = sigma)

init_params <- c(mu = 0, sigma = 1)

opt_likelihood <- optim(par = init_params, fn = likelihood, data = data)
cat("Likelihood: ", "Funktionswert =", opt_likelihood$value, " mu = ", opt_likelihood$par[1], " sigma = ", opt_likelihood$par[2], "\n")
Likelihood:  Funktionswert = -3.641176  mu =  1.40701  sigma =  0.1751672
Code 
opt_log_likelihood <- optim(par = init_params, fn = log_likelihood, data = data)
cat("Log-Likelihood: ", "Funktionswert =", opt_log_likelihood$value, " mu = ", opt_log_likelihood$par[1], " sigma = ", opt_log_likelihood$par[2], "\n")
Log-Likelihood:  Funktionswert = 0.04699389  mu =  1.407028  sigma =  0.2477029
Code 
set.seed(123)
n <- 3
mu <- 2
sigma <- 1.5
data <- rnorm(n, mean = mu, sd = sigma)

init_params <- c(mu = 0, sigma = 1)

opt_likelihood <- optim(par = init_params, fn = likelihood, data = data)
cat("Likelihood: ", "Funktionswert =", opt_likelihood$value, " mu = ", opt_likelihood$par[1], " sigma = ", opt_likelihood$par[2], "\n")
Likelihood:  Funktionswert = -1.975685e-05  mu =  2.384028  sigma =  0.8062337
Code 
opt_log_likelihood <- optim(par = init_params, fn = log_likelihood, data = data)
cat("Log-Likelihood: ", "Funktionswert =", opt_log_likelihood$value, " mu = ", opt_log_likelihood$par[1], " sigma = ", opt_log_likelihood$par[2], "\n")
Log-Likelihood:  Funktionswert = 5.258589  mu =  2.383861  sigma =  1.396321
Code 
set.seed(123)
n <- 4
mu <- 2
sigma <- 1.5
data <- rnorm(n, mean = mu, sd = sigma)

init_params <- c(mu = 0, sigma = 1)

opt_likelihood <- optim(par = init_params, fn = likelihood, data = data)
cat("Likelihood: ", "Funktionswert =", opt_likelihood$value, " mu = ", opt_likelihood$par[1], " sigma = ", opt_likelihood$par[2], "\n")
Likelihood:  Funktionswert = -3.995138e-07  mu =  2.314456  sigma =  0.6076679
Code 
opt_log_likelihood <- optim(par = init_params, fn = log_likelihood, data = data)
cat("Log-Likelihood: ", "Funktionswert =", opt_log_likelihood$value, " mu = ", opt_log_likelihood$par[1], " sigma = ", opt_log_likelihood$par[2], "\n")
Log-Likelihood:  Funktionswert = 6.455843  mu =  2.314621  sigma =  1.215455
Code 
set.seed(123)
n <- 5
mu <- 2
sigma <- 1.5
data <- rnorm(n, mean = mu, sd = sigma)

init_params <- c(mu = 0, sigma = 1)

opt_likelihood <- optim(par = init_params, fn = likelihood, data = data)
cat("Likelihood: ", "Funktionswert =", opt_likelihood$value, " mu = ", opt_likelihood$par[1], " sigma = ", opt_likelihood$par[2], "\n")
Likelihood:  Funktionswert = -3.375142e-17  mu =  0.1  sigma =  1
Code 
opt_log_likelihood <- optim(par = init_params, fn = log_likelihood, data = data)
cat("Log-Likelihood: ", "Funktionswert =", opt_log_likelihood$value, " mu = ", opt_log_likelihood$par[1], " sigma = ", opt_log_likelihood$par[2], "\n")
Log-Likelihood:  Funktionswert = 7.516858  mu =  2.290556  sigma =  1.088041

Hypothesentests

Als Beispiel wird hier der Parameter einer Exponentialverteilung geschätzt. Diese bietet sich an, da nur ein einzelner Parameter geschätzt werden muss (im Gegensatz zu z.B. der Normalverteilung, welche zwei Parameter benötigt) und somit die (Log)-Likelihood Funktion schöner geplottet werden kann.

Als Parameter wird \(\theta = 0.5\) verwendet. Die Nullhypothese wird \(H_0: \theta_0 = 0.6\) sein.

Der Wald Test betrachtet den horizontalen Abstand zwischen dem geschätzten Parameter(vektor) \(\hat{\theta}\) und dem Parameter(vektor) unter der Nullhypothese \(\theta_0\): \[t_W = \frac{\hat{\theta}- \theta_0}{\sqrt{I(\hat{\theta})^{-1}}} \sim N(0,1)\] Für einzelne Parameter ist \(I(\hat{\theta})^{-1}\) gleich der Varianz.

Code 
set.seed(4)

n <- 100
rate <- 0.5
data <- rexp(n, rate)

# Schätzen

neg_log_likelihood <- function(rate, data) {
  -sum(log(dexp(data, rate)))
}

mle_result <- optim(par = 1, fn = neg_log_likelihood, data = data, method = "BFGS", hessian = TRUE)
estimated_rate <- mle_result$par

# Testen
null_value <- 0.6

estimated_se <- sqrt(solve(mle_result$hessian[1, 1]))
wald_test_statistic <- (estimated_rate - null_value) / estimated_se

p_value <- 2 * (1 - pnorm(abs(wald_test_statistic)))
cat("Test Statistic:", wald_test_statistic, "\n", "P-value:", p_value, "\n")
Test Statistic: -1.34291 
 P-value: 0.1793012
Code 
# Plotten
log_likelihood <- function(rate, data) {
  sum(log(dexp(data, rate)))
}

rate_values <- seq(0.4, 0.8, by = 0.01)
log_likelihood_values <- sapply(rate_values, function(rate) log_likelihood(rate, data))
likelihood_plot <- data.frame(rate = rate_values, log_likelihood = log_likelihood_values)

ggplot(likelihood_plot, aes(x = rate, y = log_likelihood)) +
  geom_line() +
  labs(x = "Rate", y = "Log-Likelihood") +
  geom_vline(xintercept = null_value, linetype = "dashed")+
  annotate("text", x = (null_value + 0.01), y = -170, label = paste("Nullhypothese =", null_value), angle = 90, size = 3)+
  geom_vline(xintercept = estimated_rate, linetype = "dotted")+
  annotate("text", x = (estimated_rate - 0.01), y = -170, label = paste("geschätzter Wert =", round(estimated_rate, 2)), angle = 90, size = 3)+
  theme_bw()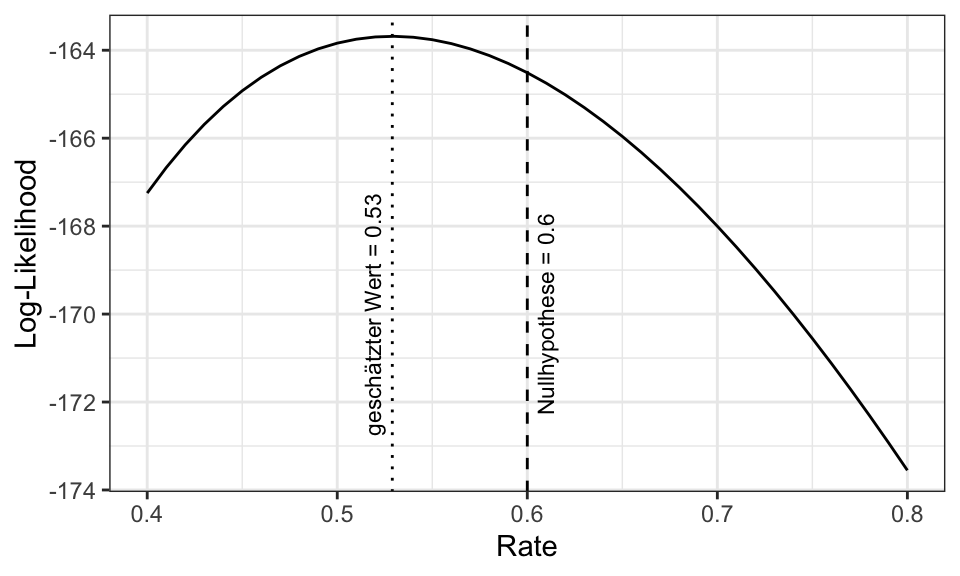

In diesem Fall kann die Nullhypothese zu einem Konfidenzlevel von 5% also nicht verworfen werden. Der geschätzte Wert liegt zu nah an dem Wert unter der Nullhypothese und es gibt zu wenige Beobachtungen.

Der Likelihood Ratio Test vergleicht den (Log)-Likelihood Wert des geschätzten Modells mit dem Wert unter der Nullhypothese: \[t_{LR} = 2(LL(\hat{\theta}) - LL(\theta_0)) \sim \chi^2(1)\]

Code 
set.seed(4)

n <- 100
rate <- 0.5
data <- rexp(n, rate)

# Schätzen

neg_log_likelihood <- function(rate, data) {
  -sum(log(dexp(data, rate)))
}

log_likelihood <- function(rate, data) {
  sum(log(dexp(data, rate)))
}

mle_result <- optim(par = 1, fn = neg_log_likelihood, data = data, method = "BFGS", hessian = TRUE)
estimated_rate <- mle_result$par

# Testen

null_value <- 0.6

log_likelihood_full <- log_likelihood(estimated_rate, data)
log_likelihood_reduced <- log_likelihood(null_value, data)
lrt_test_statistic <- 2 * (log_likelihood_full - log_likelihood_reduced)

p_value <- 1 - pchisq(lrt_test_statistic, df = 1)
cat("Test Statistic:", lrt_test_statistic, "\n", "P-value:", p_value, "\n")
Test Statistic: 1.656631 
 P-value: 0.1980588
Code 
# Plotten
rate_values <- seq(0.4, 0.8, by = 0.01)
log_likelihood_values <- sapply(rate_values, function(rate) log_likelihood(rate, data))
likelihood_plot <- data.frame(rate = rate_values, log_likelihood = log_likelihood_values)

ggplot(likelihood_plot, aes(x = rate, y = log_likelihood)) +
  geom_line() +
  geom_hline(yintercept = -mle_result$value, linetype = "dotted")+
  geom_hline(yintercept = log_likelihood_reduced, linetype = "dashed")+
  annotate("text", y = (-mle_result$value + .3), x = .7, label = paste("geschätzter Likelihood-Wert =", round(-mle_result$value, 2)), size = 3)+
  annotate("text", y = (log_likelihood_reduced - .3), x = .7, label = paste("Likelihood-Wert bei Nullhypothese =", round(log_likelihood_reduced, 2)), size = 3)+
  labs(x = "Rate", y = "Log-Likelihood") +
  theme_bw()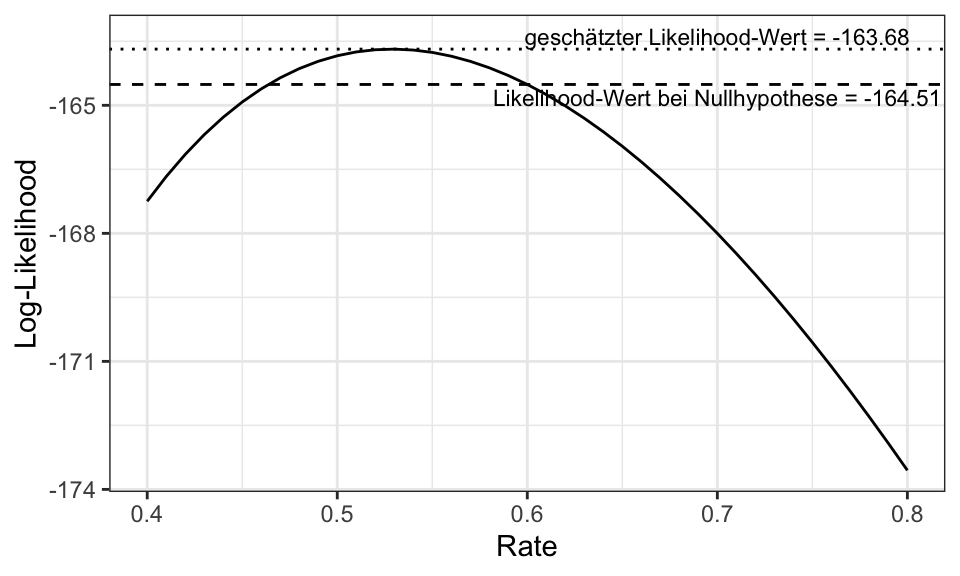

Der Lagrange Multiplier oder Score Test betrachtet die Steigung der (Log)-Likelihood Funktion unter der Nullhypothese: \[t_{LM} = \frac{g(\theta_0)}{I(\theta_0)} \sim \chi^2(1)\]

Code 
set.seed(4)

n <- 100
rate <- 0.5

data <- rexp(n, rate)

# Schätzen
neg_log_likelihood <- function(rate, data) {
  -sum(log(dexp(data, rate)))
}

log_likelihood <- function(rate, data) {
  sum(log(dexp(data, rate)))
}

mle_result <- optim(par = 1, fn = neg_log_likelihood, data = data, method = "BFGS", hessian = TRUE)
estimated_rate <- mle_result$par

# Testen
null_value <- 0.6

grad_null <- grad(func = function(rate) log_likelihood(rate, data), x = null_value)
intercept <- log_likelihood_reduced - grad_null * null_value
# hier fehlt jetzt die Fisher Informationsmatrix unter der Nullhypothese


# Plotten
rate_values <- seq(0.4, 0.8, by = 0.01)
log_likelihood_values <- sapply(rate_values, function(rate) log_likelihood(rate, data))
likelihood_plot <- data.frame(rate = rate_values, log_likelihood = log_likelihood_values)

ggplot(likelihood_plot, aes(x = rate, y = log_likelihood)) +
  geom_line() +
  geom_abline(slope = grad_null, intercept = intercept, linetype = "dashed")+
  annotate("text", y = (intercept+grad_null*0.7) + .3, x = .7, label = paste("Steigung =", round(grad_null, 2)), size = 3, angle = -30)+
  labs(x = "Rate", y = "Log-Likelihood") +
  theme_bw()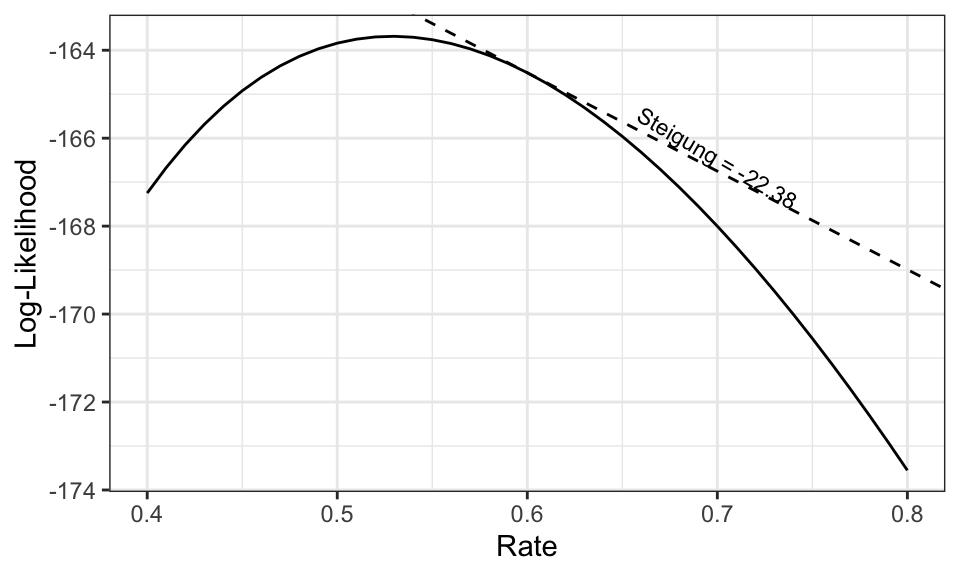

Nichtlineare Regression

Folgende Funktion kann beispielsweise nicht mit einer linearen Methode geschätzt werden: \(y_i = a \cdot sin(b x_i) + u_i\), denn die Funktion ist nicht linear im Parameter \(b\). Für die Schätzung werden Daten mit \(a = 2\), \(b = 4\) und einer Standartabweichung von \(\sigma = 0.3\) erstellt.

Code 
set.seed(4)

n <- 200

a <- 2
b <- 4

f <- function(x, a, b) a*sin(b*x)
x <- runif(n, min = 0, max = 5)
y <- f(x, a, b) + rnorm(n, mean = 0, sd = .3)

data.frame(x, y) %>%
  ggplot(aes(x = x, y = y))+
  geom_point(alpha = .5)+
  geom_function(fun = function(x) f(x, a, b))+
  theme_bw()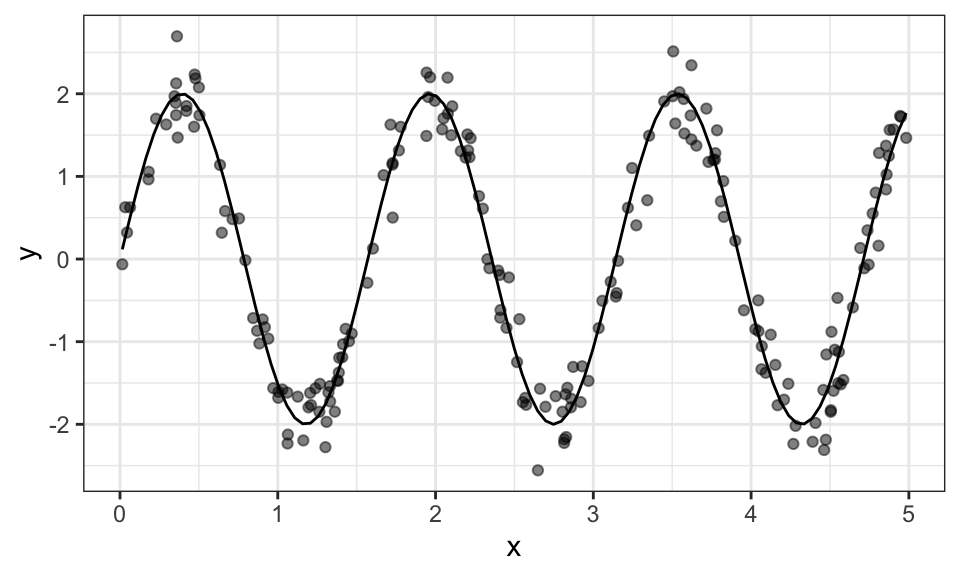

Nonlinear Least Squares

Das nichtlineare pendant zum OLS Schätzer: \(\text{min}_{\beta}SSR(\beta) = (\mathbf{y} - \mathbf{x}(\mathbf{\beta}))^\prime(\mathbf{y} - \mathbf{x}(\mathbf{\beta}))\). Man beachte den Unterschied zu OLS: \(\mathbf{y} = \mathbf{x}(\mathbf{\beta}) + \mathbf{u}\) vs \(\mathbf{y} = \mathbf{X}\mathbf{\beta} + \mathbf{u}\).

Nach der Ableitung bleibt das folgende nichtlineare Gleichungssstem: \(\mathbf{X}(\mathbf{\beta})^\prime(\mathbf{y}-\mathbf{x}(\mathbf{\beta}))=\mathbf{0}\)

Code 
R <- nls(y ~ f(x, a, b), start = list(a = 1, b = 3.5))
summary(R)

Formula: y ~ f(x, a, b)

Parameters:
  Estimate Std. Error t value Pr(>|t|)    
a 1.983842   0.029283   67.75   <2e-16 ***
b 3.995111   0.004891  816.80   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2964 on 198 degrees of freedom

Number of iterations to convergence: 6 
Achieved convergence tolerance: 1.213e-06
Code 
data.frame(x,y) %>%
  ggplot(aes(x = x, y = y))+
  geom_point(alpha = .2)+
  geom_function(fun = function(x) coef(R)[1]*sin(coef(R)[2]*x))+
  theme_bw()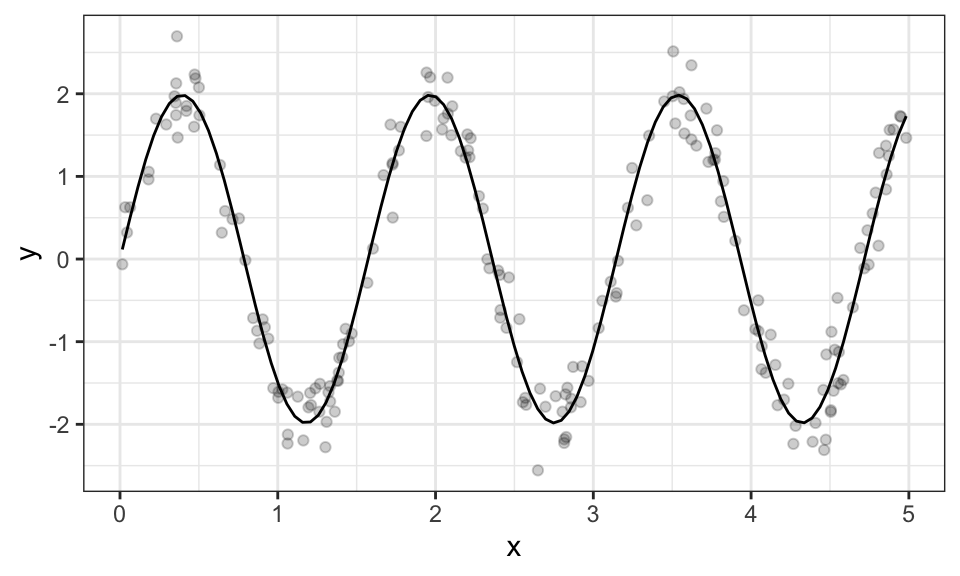

Nichtlineare Schätzer, auch NLS, sind sensibel was die Startwerte der numerischen Optimierung angeht. Mehr dazu folgt unten.

Maximum-Likelihood-Schätzung

Für eine ML Schätzung wird die folgende Likelihood Funktion maximiert: \[L(a, b, \sigma) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\left(-\frac{(y_i - f(x_i, a, b))^2}{2\sigma^{2}}\right)\] Für leichtere Ableitungen wird die Funktion typischerweise log-Transformiert. Da der Logarithmus eine streng monotone Funktion ist, bleiben Extremstellen nach einer log-Transformation gleich. \[LL(a, b, \sigma) = \sum_{i=1}^{n} \left(-\frac{1}{2}\log(2\pi\sigma^{2}) - \frac{(y_i - f(x_i, a, b))^2}{2\sigma^{2}}\right)\] Da die hier für die numerische Optimierung genutzte optim() Funktion ein Minimum sucht, wird die negative LL Funktion verwendet.

Code 
neg_log_likelihood <- function(params, x, y) {
  a <- params[1]
  b <- params[2]
  sigma <- params[3]
  
  y_pred <- f(x, a, b)
  
  neg_ll <- -sum(-0.5*log(2*pi*sigma^2) - 0.5*((y - y_pred)^2)/(sigma^2))
  #neg_ll <- -sum(dnorm(y, mean = y_pred, sd = sigma, log = TRUE)) # Alternative
  return(neg_ll)
}

init_params <- c(a = 1, b = 3.5, sigma = 0.5)

opt_result <- optim(par = init_params, fn = neg_log_likelihood, x = x, y = y)
opt_result$par
        a         b     sigma 
1.9838290 3.9951124 0.2949199

Für die hier gewählten Startwerte \(a=1\) und \(b=3.5\) findet der Schätzer die wahren Werte ziemlich gut. Für beispielsweise \(a=1\) und \(b=2\) jedoch werden falsche Werte gefunden:

Code 
init_params <- c(a = 1, b = 2, sigma = 0.5)

opt_result <- optim(par = init_params, fn = neg_log_likelihood, x = x, y = y)
opt_result$par
        a         b     sigma 
0.1504887 2.4726679 1.4475354

Dagegen scheinen verschiedene Startwerte für \(a\) kein Problem zu sein. Das liegt wohl daran, dass \(a\) in dem Modell linear ist. Ein Beispiel mit \(a=10\) und \(b=3.5\):

Code 
init_params <- c(a = 10, b = 3.5, sigma = 0.5)

opt_result <- optim(par = init_params, fn = neg_log_likelihood, x = x, y = y)
opt_result$par
        a         b     sigma 
1.9838073 3.9951363 0.2949901

Der folgende Plot zeigt das Problem. Es wird die resultierende negative Log-Likelihood Funktion dargestellt (für \(a = 2\) und \(\sigma = 0.3\). Für diese wird von der optim() Funktion ausgehend von den Startwerten numerisch ein Minimum gesucht. Da die Funktion jedoch viele lokale Minima hat, sind die Startwerte essentiell. Startet man beispielsweise von \(b = 2\), so wird nur das lokale Minimum bei \(b \approx 2.5\) gefunden.

Code 
b_values <- seq(-1, 5, by = 0.01)
neg_ll_values <- numeric(length(b_values))
a <- 2
sigma <- 0.3

for (i in seq_along(b_values)) {
  neg_ll_values[i] <- neg_log_likelihood(c(a, b_values[i], sigma), x, y)
}

data.frame(b_values, neg_ll_values) %>%
  ggplot(aes(x = b_values, y = neg_ll_values))+
  geom_line()+
  geom_vline(xintercept = 4, linetype = "dashed")+
  theme_bw()+
  labs(x = "b",
       y = "Negative LL Wert")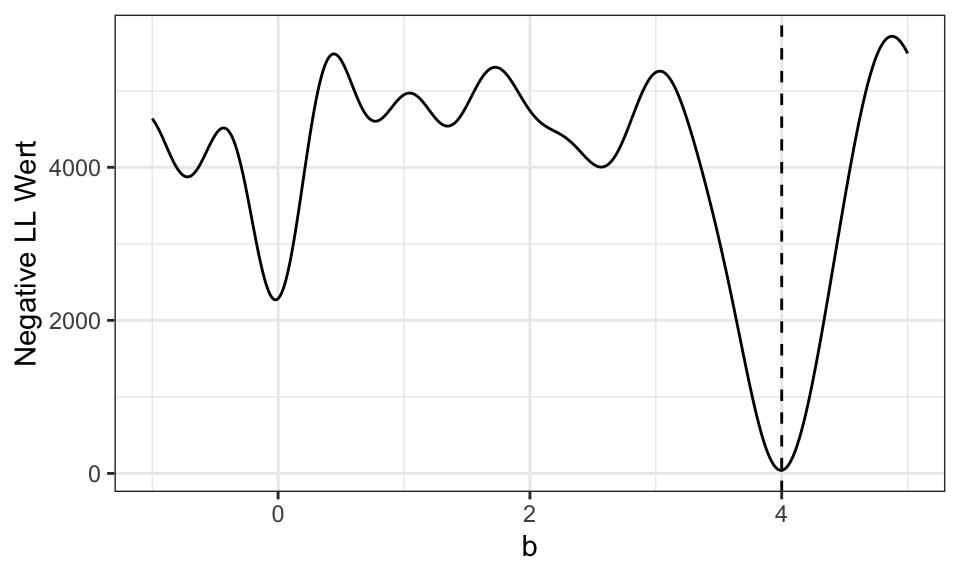

Künstliche Regression

Künstiliche Regressionen sind lineare Regressionen, die aus nichtlinearen Modellen gewonnen werden, um Berechnungen und Tests zu vereinfachen.

Gauss-Newton-Regression

Die Gauss-Newton-Regression ist ein iteratives Verfahren zur Schätzung der Parameter in nichtlinearen Regressionsmodellen. Es basiert auf einer linearen Approximation der nichtlinearen Funktion und verwendet die Methode der kleinsten Quadrate, um die Parameter zu schätzen.

Modell

Das nichtlineare Regressionsmodell kann wie folgt definiert werden:

\[ y_i = f(x_i, \mathbf{\beta}) + \epsilon_i \]

wo \(y_i\) die beobachtete abhängige Variable ist, \(x_i\) der Vektor der unabhängigen Variablen, \(\mathbf{\beta}\) der Vektor der zu schätzenden Parameter, \(f(x_i, \mathbf{\beta})\) die nichtlineare Funktion und \(\epsilon_i\) der Fehlerterm.

Es wird weiterhin das Beispiel von oben verwendet: \(y_i = a \cdot sin(b x_i) + u_i\) mit \(a=2\) und \(b=4\).

Gauss-Newton-Algorithmus

Der Gauss-Newton-Algorithmus verwendet eine iterative Methode, um die Parameter \(\mathbf{\beta}\) schrittweise zu verbessern. Der Algorithmus basiert auf einer linearen Approximation der Funktion \(f(x_i, \mathbf{\beta})\) um die aktuellen Schätzwerte \(\mathbf{\beta}^{(k)}\). Die lineare Approximation kann mit Hilfe des Taylor-Polynoms erster Ordnung durchgeführt werden: \[ f(x_i, \mathbf{\beta}) \approx f(x_i, \mathbf{\beta}^{(k)}) + \mathbf{J} \cdot (\mathbf{\beta} - \mathbf{\beta}^{(k)}) \]

wobei \(\mathbf{J}\) die Jacobimatrix der Funktion \(f(x_i, \mathbf{\beta})\) ist. Die Jacobimatrix enthält die partiellen Ableitungen von \(f\) nach den Parametern \(\mathbf{\beta}\).

Die Schätzung der Parameter \(\mathbf{\beta}\) wird dann durch Minimierung der Fehlerquadrate erreicht: \[ \min_{\mathbf{\beta}} \sum_{i=1}^{n} \left( y_i - f(x_i, \mathbf{\beta}^{(k)}) - \mathbf{J} \cdot (\mathbf{\beta} - \mathbf{\beta}^{(k)}) \right)^2 \]

Der Gauss-Newton-Algorithmus verwendet die Methode der kleinsten Quadrate, um die Parameter \(\mathbf{\beta}\) zu schätzen, indem er die obige Zielfunktion iterativ minimiert. Die Iteration erfolgt wie folgt:

  1. Initialisierung der Parameter \(\mathbf{\beta}^{(0)}\)

  2. Berechnung der Jacobimatrix \(\mathbf{J}\) und des Residuals \(\mathbf{r} = \mathbf{y} - f(\mathbf{x}, \mathbf{\beta}^{(k)})\)

  3. Berechnung der Aktualisierung der Parameter \(\Delta \mathbf{\beta}\): \[ \Delta \mathbf{\beta} = (\mathbf{J}^T \cdot \mathbf{J})^{-1} \cdot \mathbf{J}^T \cdot \mathbf{r} \]

  4. Aktualisierung der Parameter: \[ \mathbf{\beta}^{(k+1)} = \mathbf{\beta}^{(k)} + \Delta \mathbf{\beta} \]

  5. Wiederholung der Schritte 2-4 bis ein Abbruchkriterium erfüllt ist (z. B. Konvergenz oder maximale Anzahl an Iterationen)

Code 
set.seed(4)
n <- 200
a <- 2
b <- 4

# Definition Funktion und Ableitungen nach a und b
f <- function(x, a, b) a*sin(b*x)
f_a <- function(x, a, b) sin(b*x)
f_b <- function(x, a, b) a*x*sin(b*x)

x <- runif(n, min = 0, max = 5)
y <- f(x, a, b) + rnorm(n, mean = 0, sd = .3)

betahat <- c(1, 3.5) # Startwerte
iter <- 0
repeat
{
 beta1 <- betahat[1]
 beta2 <- betahat[2]
 
 J <- cbind(f_a(x, beta1, beta2), f_b(x, beta1, beta2))
 r <- y - f(x, beta1, beta2)
 new_betahat <- betahat + solve(t(J) %*% J) %*% t(J) %*% r
 
 iter <- iter + 1
 
 # Abbruchkriterien
 if (sum((betahat - new_betahat)^2) < 1e-5){
   cat("Abbruch wegen Konvergenz \n")
   break
 }
 if (iter > 50){
   cat("Abbruch wegen Iterationen \n")
   break
 }
 
 betahat <- new_betahat
} 
Abbruch wegen Konvergenz
Code 
betahat
         [,1]
[1,] 1.972976
[2,] 4.024437
Code 
data.frame(x,y) %>%
  ggplot(aes(x = x, y = y))+
  geom_point(alpha = .2)+
  geom_function(fun = function(x) betahat[1]*sin(betahat[2]*x))+
  theme_bw()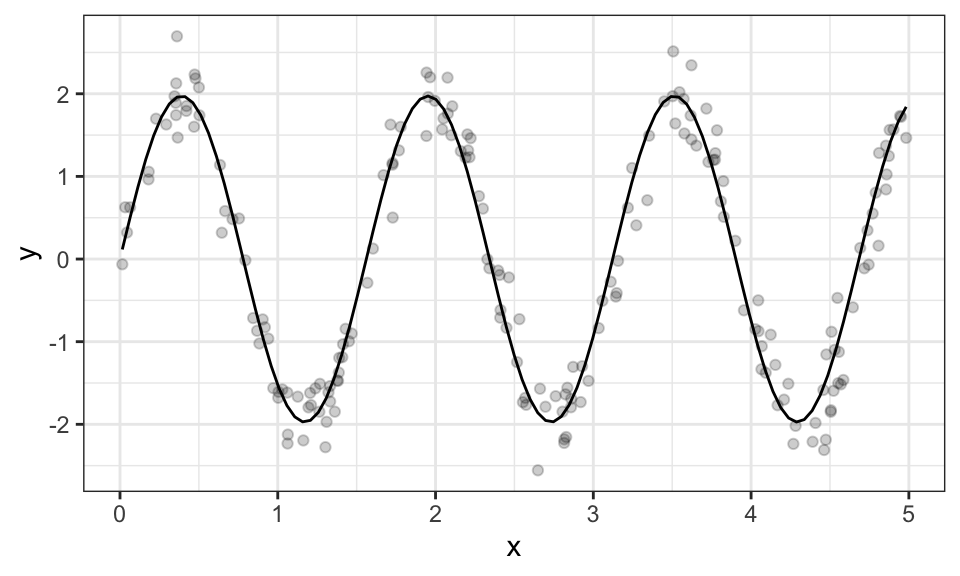

Instrumentvaraiblen Schätzung

Eine Instrumentvariablenschätzung bietet sich dort an, wo die Annahme \(\text{Cov}(x, u)\) verletzt ist. Es muss dann ein Instrument \(w\) gefunden werden, welches die folgenden Annahmen erfüllt:

  • \(\text{Cov}(w, x) \neq 0\) (Relevanz): Diese Annahme ist meist unkritisch, da sie einfach getestet werden kann, z.B. durch eine Regression von \(w\) auf \(x\).
  • \(\text{Cov}(w, u) = 0\) (Validität): Diese Annahme ist schwieriger, da sie (in der Realität) nicht getestet werden kann, weil die Fehler \(u\) nicht beobachtet werden. Daher muss hier eine (ökonomische) Begründung gefunden werden.

Beispiel: Messfehler in x

Durch Messfehler in der erklärenden Variable \(x_\text{observed} = x_\text{true} + u_x\) entsteht ein Bias gegen Null in einer einfachen OLS Schätzung. Aushelfen kann dabei ein Instrument \(w\). Dieses darf nicht mit den Fehlertermen \(u_\text{hat}\) aus der Regression korrelieren (Validität) und muss mit \(x_\text{observed}\) korrelieren (Relevanz).

Ein Beispiel hierfür wäre

  • \(x_\text{true}\): Humankapital
  • \(x_\text{observed}\): Angabe zu Schuljahren, mit “Messfehlern”
  • \(y\): Gehalt (abhängig von \(x_{true}\))

Eine Regression nur mit \(x_\text{observed}\) und \(y\) wäre verzerrt, da der Fehlerterm \(v\) nun auch \(\beta_2\) enthält: \[ \begin{align*} y &= \beta_1 + \beta_2 x_\text{true} + u \qquad \text{mit } x_\text{observed} = x_\text{true} + v \\ &= \beta_1 + \beta_2 (x_\text{observed} - v) + u \\ &= \beta_1 + \beta_2 x_\text{observed} + (u - \beta_2v) \qquad \text{mit } \epsilon = u - \beta_2v \\ &= \beta_1 + \beta_2 x_\text{observed} + \epsilon \\ \end{align*} \]

Daher kann ein Instrument \(w\) eingeführt werden, z.B. die Anzahl der Schuljahre der Eltern. \(w\) dürfte in diesem Fall nicht mit dem Fehler in der Umfrage zusammenhängen und ist wahrscheinlich hoch korreliert mit dem Humankapital \(x\).

Code 
n <- 100
n_runs <- 10000
beta <- matrix(rep(0, 3*n_runs), ncol = 3)

for(i in 1:n_runs){
  x_true <- seq(from = 0, to = 10, length.out = n)
  u_x <- rnorm(n, mean = 0, sd = 1)
  x_observed <- x_true + u_x
  
  u_y <- rnorm(n, mean = 0, sd = 1)
  y <- 2 + 4*x_true + u_y
  
  u_w <- rnorm(n, mean = 0, sd = 1)
  w <- 0.8*x_true + u_w
  
  beta[i,1] <- coef(lm(y ~ x_true))[2] # Wahres Modell
  beta[i,2] <- coef(lm(y ~ x_observed))[2] # Falsches Modell
  beta[i,3] <- coef(tsls(y ~ x_observed, ~w))[2] # IV
}

beta %>%
  data.frame() %>%
  rename("Wahres Modell" = X1, "Falsches Modell" = X2, "IV Schätzung" = X3) %>%
  pivot_longer(cols = everything(), names_to = "modell", values_to = "beta2") %>%
  ggplot(aes(x = beta2, color = modell))+
  geom_density()+
  geom_vline(xintercept = 4, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top",
        legend.title = element_blank())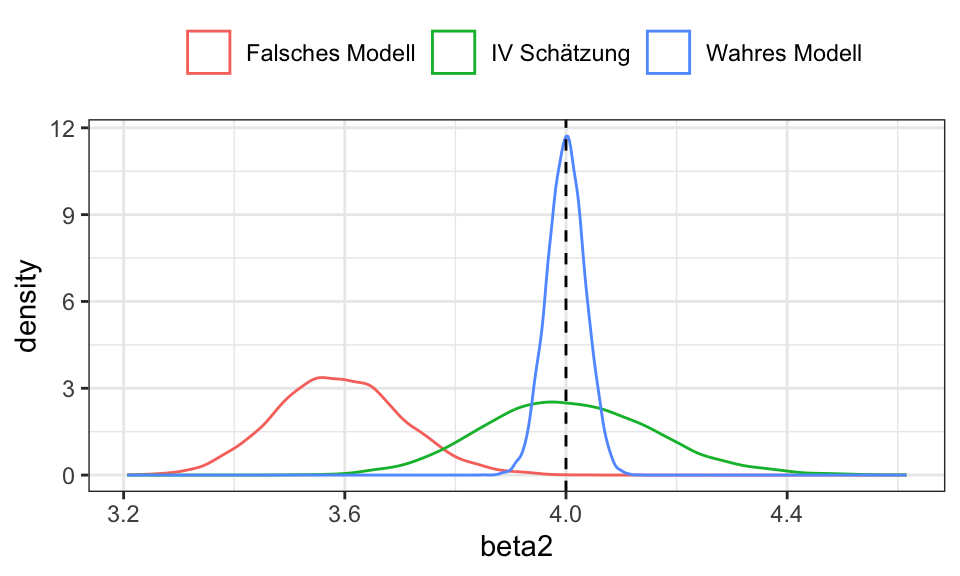

Wie man sehen kann ist die einfache OLS Schätzung zu Null verzerrt. Das ist immer der Fall, auch wenn \(\beta_{2, \text{wahr}}\) negativ wäre.

Die Instrumentvariablenschätzung trifft zwar im Mittel den wahren Wert von \(\beta_2\), weißt aber eine höhere Varianz auf als die OLS Schätzung des wahren Modells (ohne Messfehler).

ACHTUNG: Das hier vorgestellte Beispiel bezieht sich nur auf Messfehler in \(x\), nicht auf andere unberücksichtigte Einflüsse auf das Gehalt wie z.B. Intelligenz oder Durchhaltevermögen, welche ebenfalls durch \(u_y\) aufgefangen werden. Dafür wäre die Anzahl der Schuljahre der Eltern wahrscheinlich kein gutes Instrument, weil die Anzahl der Schuljahre der Eltern und die Intelligenz der beobachteten Person wahrscheinlich korrelieren.

Beispiel: Endogene Regressoren

Wahres Modell \(y_i = \beta_1 + \beta_2 x_i + \beta_3 z_i\) wobei

  • \(y_i\): Einkommen
  • \(x_i\): Schuliche & Akademische Ausbildung (Jahre)
  • \(z_i\): Allgemeine Fähigkeit

Allerdings wird die Fähigkeit \(z\) nicht beobachtet und \(\text{Cov}(x,z) = 0.7\). Bei einer “naiven” Regression von \(y\) auf \(x\) fällt somit \(z\) in den Fehlerterm \(u\). Das führt zu einer Verzerrung von \(\beta_2\).

Ein Instrument \(w\) könnte die Entfernung zwischen dem Wohnort und der nächsten Universität sein. Die Idee hier ist, dass Personen, die näher an einer Universität wohnen diese auch eher besuchen (z.B. weil es günstiger ist, da sie bei den Eltern wohnen bleiben können) und somit eine längere Ausbildung haben. Mit der Fähigkeit oder dem Lohn sollte diese Entfernung jedoch nicht zusammenhängen.

Code 
n <- 100
n_runs <- 1000
beta <- matrix(rep(0, 3*n_runs), ncol = 3)

for(i in 1:n_runs){
  Sigma <- rbind(c(3, 0.7), 
                 c(0.7, 3))
  mu <- c(10, 20)
  
  x_z <- MASS::mvrnorm(n, mu, Sigma)
  x <- x_z[,1]
  z <- x_z[,2]
  u <- rnorm(n, mean = 0, sd = 2)
  
  y <- 2 + 4*x + 6*z + u
  
  w <- residuals(lm(x ~ z)) + rnorm(n, mean = 0, sd = 1)
  
  beta[i,1] <- coef(lm(y ~ x+z))[2] # True model
  beta[i,2] <- coef(lm(y ~ x))[2] # Model with endogenous regressor
  beta[i,3] <- coef(tsls(y ~ x, ~w))[2] # IV regression
}

beta %>%
  data.frame() %>%
  rename("Wahres Modell" = X1, "Falsches Modell" = X2, "IV Schätzung" = X3) %>%
  pivot_longer(cols = everything(), names_to = "modell", values_to = "beta2") %>%
  #filter(modell != "Wahres Modell") %>%
  ggplot(aes(x = beta2, color = modell))+
  geom_density()+
  geom_vline(xintercept = 4, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top",
        legend.title = element_blank())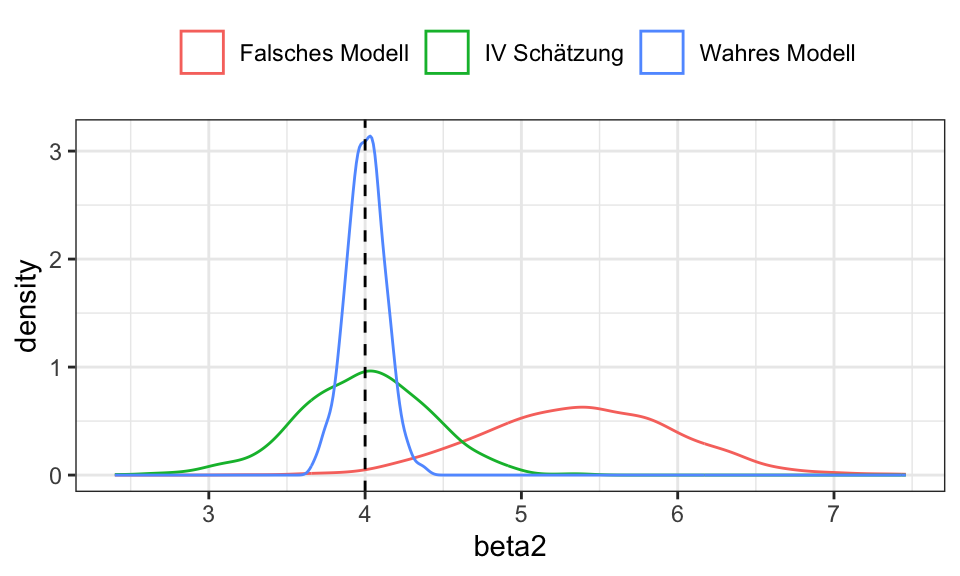

In dem falschen Regression von \(y\) (nur) auf \(x\) entsteht eine Korrelation zwischen \(y\) und \(u\): \(\text{Cov}(y,u) \neq 0\). \(w\) und \(x\) sind hoch korreliert \(\text{Cov}(y,u) \neq 0\).

Wieso ist cor(y, resid(tsls(y ~ x, ~w)) so hoch?

Verallgemeinerte Momentenschätzung

Bei der Momentenschätzung werden (zentrierte) Populationsmomente geschätzt um aus diesen die Parameter einer Verteilung zu gewinnen.

Im folgenden wird \(r\) für die Anzahl der Momentgleichungen und \(k\) für die Anzahl der zu schätzenden Parameter einer Verteilung verwendet.

Klassische Momentenmethode (CMM)

Für CMM gilt \(r = k\).

In einem Beispiel mit der Normalverteilung wären sind der Erwartungswert als das erste Moment \(\mu = E(x)\) und die Varinaz als das zweite Moment \(\sigma^2 = E((x-\mu)^2)\) interessant:

Code 
set.seed(1)

n <- 100
x <- rnorm(n, mean = 2, sd = 1)

m1 <- 1/n * sum(x)
m2 <- 1/n * sum((x - m1)^2)

cat("Erwartungswert (1. Moment) =", round(m1, 2),
    "\nVarianz (2. zentriertes Moment) =", round(m2, 2), "\n")
Erwartungswert (1. Moment) = 2.11 
Varianz (2. zentriertes Moment) = 0.8
Code 
data.frame(x) %>%
  ggplot(aes(x = x))+
  geom_line(stat = "density", alpha = .6, color = "blue")+
  geom_vline(xintercept = m1, linetype = "dashed")+
  geom_vline(xintercept = c(m1+m2, m1-m2), linetype = "dotted")+
  geom_function(fun = function(x) dnorm(x, mean = m1, sd = sqrt(m2)))+
  theme_bw()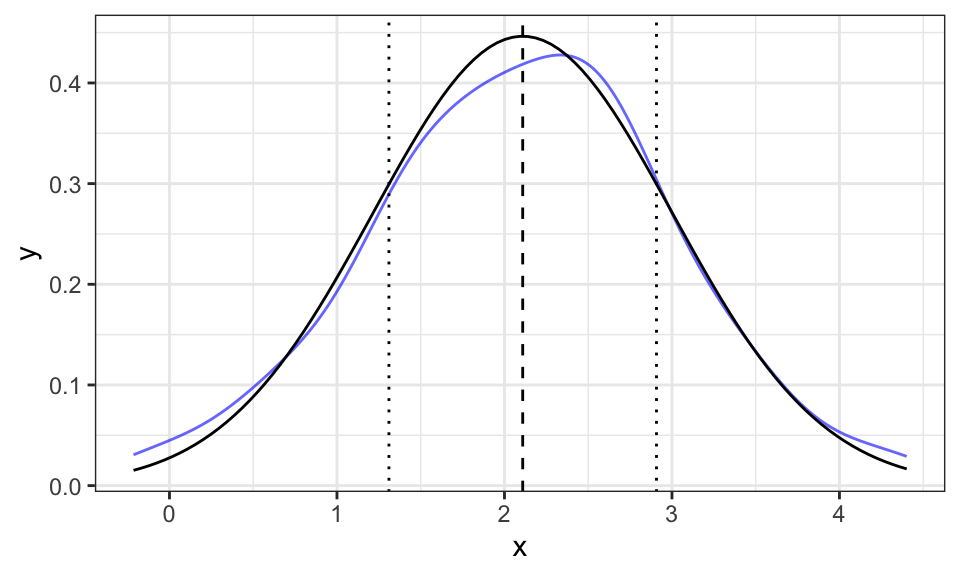

Die gestrichelte Linie stellt die Schätzung für \(E(x)\) dar, die gepunkteten stellen \(E(x^2)\) dar.

Allgemein wird mit \(\mu_j(\mathbf{\theta})\) das \(j\)te Polulationsmoment und \(\frac{1}{n}\sum_{i=1}^n x^j\) das \(j\)te Stichprobenmoment betrachtet. Der Parametervektor \(\theta\) soll so gewählt werden, dass \[ \mu_j(\mathbf{\theta}) = \frac{1}{n}\sum x^j \Leftrightarrow \mu_j(\mathbf{\theta}) - \frac{1}{n}\sum x^j = 0 \] Das kann nun als Gleichungssystem für die \(k\) Parameter geschrieben werden: \[ \mathbf{m}(\mathbf{\theta}) = \begin{bmatrix} m_1(\mathbf{\theta}) \\ m_2(\mathbf{\theta}) \\ \vdots \\ m_k(\mathbf{\theta}) \end{bmatrix} = \begin{bmatrix} \mu_1(\mathbf{\theta}) - \frac{1}{n}\sum x^1 \\ \mu_2(\mathbf{\theta}) - \frac{1}{n}\sum x^2 \\ \vdots \\ \mu_k(\mathbf{\theta}) - \frac{1}{n}\sum x^k \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \mathbf{0} \]

Ein solches Gleichungssystem kann exakt gelöst werden, da die Anzahl der Unbekannten gleich der Anzahl der Gleichungen ist.

Verallgemeinerte Momentenmethode (GMM)

In GMM gilt \(r > k\).

Es wird ebenfalls das Gleichungssystem \(\mathbf{m}(\mathbf{\theta}) = \mathbf{0}\) aufgestellt. Nur dieses lässt sich nicht exakt lösen, da die Anzahl der Gleichungen die Zahl der zu schätzenden Parameter übersteigt. Daher muss eine Zielfunktion her, welche die Summe der gewichteten Momentengleichungen minimiert: \[ \hat{\mathbf{\theta}} = \text{argmin}_\mathbf{\theta} Q(\mathbf{\theta}) = \mathbf{m}(\mathbf{\theta})^\prime \mathbf{A} \mathbf{m}(\mathbf{\theta}) \]

Wie das funktioniert wird nun Anhand des Beispiels mit der Normalverteilung gezeigt. Diesmal werden jedoch die ersten 3 Momente verwendet (\(r=3 > k=2\)).

Code 
n <- 1000
x <- rnorm(n, mean = 4, sd = 2)

# Stichprobenmomente
m1 <- 1/n * sum(x)
m2 <- 1/n * sum((x - m1)^2)
m3 <- 1/n * sum((x - m1)^3)

# Gewichtungsmatrix
A <- rbind(c(1,0,0),
           c(0,1,0),
           c(0,0,1))

gmm_criterion <- function(params) {
    mu <- params[1]
    sigma <- params[2]

    # Polulationsmomente
    t1 <- mu
    t2 <- sigma^2
    t3 <- 0 # Schiefe (3. Moment) der Normalverteilung ist 0

    # Momentengleichungen
    m <- c(m1 - t1, 
           m2 - t2, 
           m3 - t3)

    # Zielfunktion mit Gewichtung A
    gmm_obj <- t(m) %*% A %*% m
    return(gmm_obj)
}

init_params <- c(mean = 1, sd = 1) # sd muss größer Null sein
res <- optim(init_params, gmm_criterion, method = "BFGS")

res$par
    mean       sd 
3.952863 2.091397

Vergleich GMM und ML

Code 
n <- 100
n_runs <- 1000
results <- cbind(numeric(n_runs), numeric(n_runs))

exp_rate <- 2

init_param_gmm <- 1
init_param_ml <- 1

# Gewichtungsmatrix
A <- rbind(c(1,0,0),
           c(0,1,0),
           c(0,0,1))

for(i in 1:n_runs){
  x <- rexp(n, rate = exp_rate)

  # GMM
  # Stichprobenmomente
  m1 <- 1/n * sum(x)
  m2 <- 1/n * sum((x - m1)^2)
  m3 <- 1/n * sum((x - m1)^3)
  
  gmm_criterion <- function(param) {
      lambda <- param[1]
  
      # Polulationsmomente
      t1 <- 1/lambda
      t2 <- 1/lambda^2
      t3 <- 2
  
      # Momentengleichungen
      diff <- c(m1 - t1, 
                m2 - t2, 
                m3 - t3)
  
      # Zielfunktion mit Gewichtung A
      gmm_obj <- t(diff) %*% A %*% diff
      return(gmm_obj)
  }
  
  res_gmm <- optim(init_param_gmm, gmm_criterion, method = "BFGS")
  results[i,1] <- res_gmm$par
  
  
  # ML
  log_likelihood <- function(param) {
    lambda <- param[1]

    logL <- n * log(lambda) - lambda * sum(x)
    return(-logL)  # Negative, weil optim() Minimum sucht
  }
  
  res_ml <- optim(init_param_ml, log_likelihood, method = "BFGS")
  results[i,2] <- res_ml$par
}

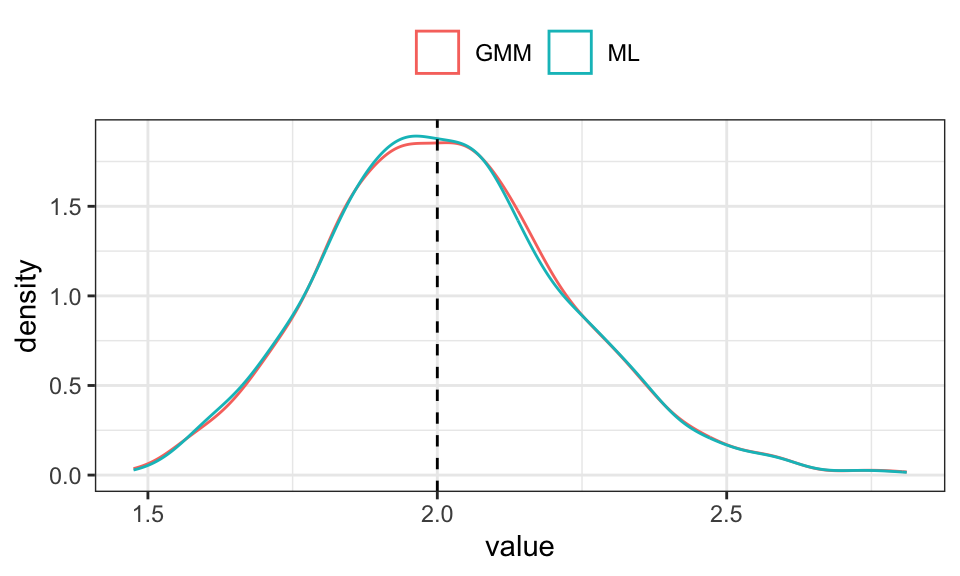
results %>%
  data.frame() %>%
  rename("GMM" = X1, "ML" = X2) %>%
  pivot_longer(cols = everything()) %>%
  ggplot(aes(x = value, color = name))+
  geom_density()+
  geom_vline(xintercept = exp_rate, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top",
        legend.title = element_blank())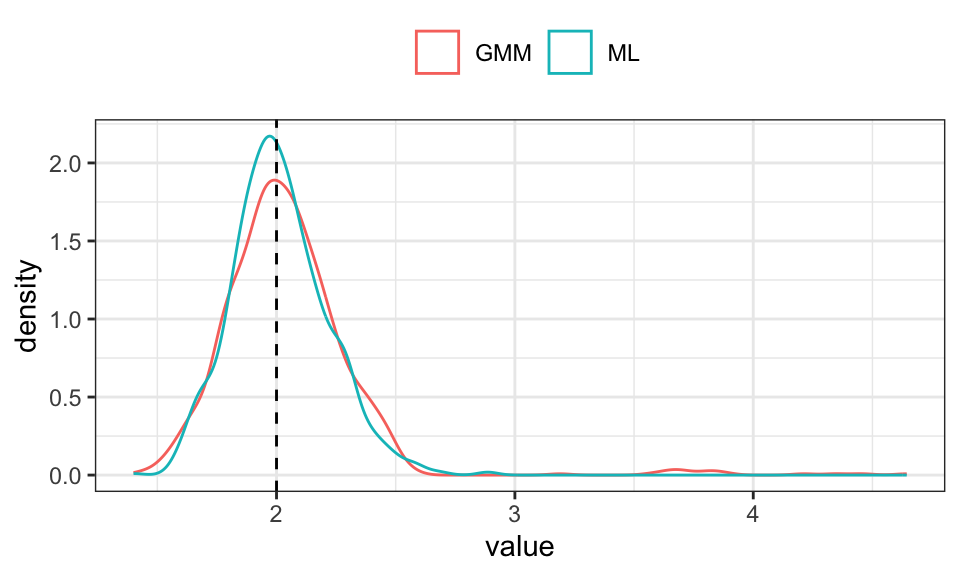

Code 
n <- 100
n_runs <- 1000
results <- cbind(numeric(n_runs), numeric(n_runs))

exp_rate <- 2

init_param_gmm <- 1
init_param_ml <- 1

# Gewichtungsmatrix
A <- rbind(c(2,0,0),
           c(0,0.8,0),
           c(0,0,0.2))

for(i in 1:n_runs){
  x <- rexp(n, rate = exp_rate)

  # GMM
  # Stichprobenmomente
  m1 <- 1/n * sum(x)
  m2 <- 1/n * sum((x - m1)^2)
  m3 <- 1/n * sum((x - m1)^3)
  
  gmm_criterion <- function(param) {
      lambda <- param[1]
  
      # Polulationsmomente
      t1 <- 1/lambda
      t2 <- 1/lambda^2
      t3 <- 2
  
      # Momentengleichungen
      diff <- c(m1 - t1, 
                m2 - t2, 
                m3 - t3)
  
      # Zielfunktion mit Gewichtung A
      gmm_obj <- t(diff) %*% A %*% diff
      return(gmm_obj)
  }
  
  res_gmm <- optim(init_param_gmm, gmm_criterion, method = "BFGS")
  results[i,1] <- res_gmm$par
  
  
  # ML
  log_likelihood <- function(param) {
    lambda <- param[1]

    logL <- n * log(lambda) - lambda * sum(x)
    return(-logL)  # Negative, weil optim() Minimum sucht
  }
  
  res_ml <- optim(init_param_ml, log_likelihood, method = "BFGS")
  results[i,2] <- res_ml$par
}

results %>%
  data.frame() %>%
  rename("GMM" = X1, "ML" = X2) %>%
  pivot_longer(cols = everything()) %>%
  ggplot(aes(x = value, color = name))+
  geom_density()+
  geom_vline(xintercept = exp_rate, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top",
        legend.title = element_blank())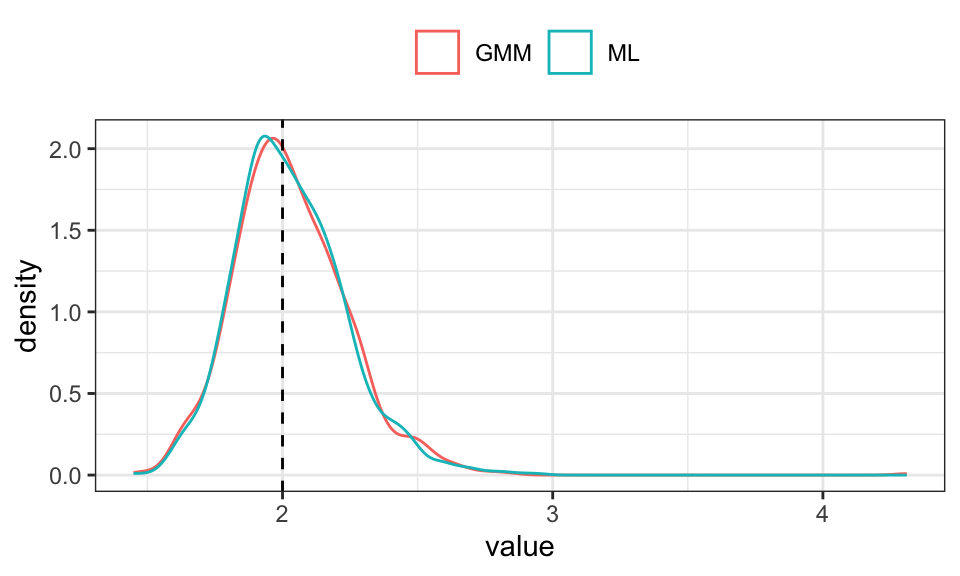

Code 
n <- 100
n_runs <- 1000
results <- cbind(numeric(n_runs), numeric(n_runs))

exp_rate <- 2

init_param_gmm <- 1
init_param_ml <- 1

# Gewichtungsmatrix
A <- rbind(c(2.7,0,0),
           c(0,0.2,0),
           c(0,0,0.1))

for(i in 1:n_runs){
  x <- rexp(n, rate = exp_rate)

  # GMM
  # Stichprobenmomente
  m1 <- 1/n * sum(x)
  m2 <- 1/n * sum((x - m1)^2)
  m3 <- 1/n * sum((x - m1)^3)
  
  gmm_criterion <- function(param) {
      lambda <- param[1]
  
      # Polulationsmomente
      t1 <- 1/lambda
      t2 <- 1/lambda^2
      t3 <- 2
  
      # Momentengleichungen
      diff <- c(m1 - t1, 
                m2 - t2, 
                m3 - t3)
  
      # Zielfunktion mit Gewichtung A
      gmm_obj <- t(diff) %*% A %*% diff
      return(gmm_obj)
  }
  
  res_gmm <- optim(init_param_gmm, gmm_criterion, method = "BFGS")
  results[i,1] <- res_gmm$par
  
  
  # ML
  log_likelihood <- function(param) {
    lambda <- param[1]

    logL <- n * log(lambda) - lambda * sum(x)
    return(-logL)  # Negative, weil optim() Minimum sucht
  }
  
  res_ml <- optim(init_param_ml, log_likelihood, method = "BFGS")
  results[i,2] <- res_ml$par
}

results %>%
  data.frame() %>%
  rename("GMM" = X1, "ML" = X2) %>%
  pivot_longer(cols = everything()) %>%
  ggplot(aes(x = value, color = name))+
  geom_density()+
  geom_vline(xintercept = exp_rate, linetype = "dashed")+
  theme_bw()+
  theme(legend.position = "top",
        legend.title = element_blank())